Mathematik Nachhilfe in Düsseldorf - Lernzentrum Köpper - Trigonometrie

Hier klicken und
Nachhilfe in Mathematik
kostenlos kennenlernen

Der Kosinussatz

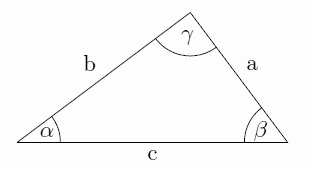
Der Kosinussatz ist eine Verallgemeinerung des Satzes von Pythagoras auf beliebige (also insbesondere nicht-rechtwinklige) Dreiecke. In dem nebenstehenden Dreieck gilt bei \gamma = 90° nach dem Satz des Pythagoras

c^2 = a^2 + b^2.

Der Kosinussatz gilt für ein beliebiges \gamma und besagt

c^2 = a^2 + b^2 - 2ab \cos \gamma.

Er findet seine Anwendung, wenn von einem Dreieck zwei Seiten und der eingeschlossene Winkel oder wenn drei Seiten gegeben sind. In letzterem Fall löst man ihn nach \cos \gamma auf:

\cos \gamma = \frac{a^2 + b^2 - c^2}{2ab}.

Wir geben einen Beweis des Kosinussatzes zunächst für \gamma < 90°. Dazu betrachten wir a, b und \gamma als gegeben und zeigen, wie man daraus c berechnet.

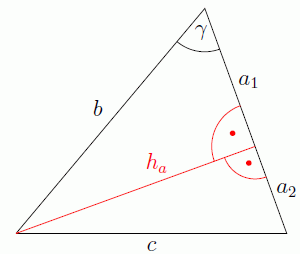
Wir zeichnen die Höhe h_a auf die Seite a ein und teilen a damit in die Abschnitte a_1 und a_2 auf. Es entstehen zwei rechtwinklige Teildreiecke. In dem oberen Teildreieck berechnen wir mit dem Kosinus-Seitenverhältnis die Länge von a_1 und dann mit dem Satz des Pythagoras die Länge der Höhe h_a. Dann berechnen wir a_2, indem wir a_1 von a abziehen. Schließlich können wir wieder mit dem Satz des Pythagoras aus a_2 und h_a die gesuchte Seite c berechnen:

\begin{align*} a_1 &= b \nachhilfe \cos \gamma &&\text{mit dem Kosinus-Seitenverhältnis} \\[3pt] h_a^2 &= b^2 - a_1^2 = b^2 - b^2 \nachhilfe \cos^2 \gamma &&\text{nach Pythagoras}\\[3pt] a_2 &= a - a_1 = a - b \nachhilfe \cos \gamma &&\text{denn $a = a_1 + a_2$} \\[3pt] c^2 &= h_a^2 + a_2^2 &&\text{nach Pythagoras} \\[3pt] &= b^2 - b^2 \nachhilfe \cos^2 \gamma + (a - b \nachhilfe \cos \gamma)^2 &&\text{für $h_a^2$ und $a_2^2$ eingesetzt}\\[3pt] &= b^2 - b^2 \nachhilfe \cos^2 \gamma + a^2 - 2ab \nachhilfe \cos \gamma + b^2 \cos^2 \gamma &&\text{mit der binomischen Formel aufgelöst} \\[3pt] &= b^2 + a^2 - 2ab \nachhilfe \cos \gamma. \end{align*}

Für \gamma = 90° ergibt sich wegen \cos \gamma = 0 der Satz des Pythagoras, den wir hier nicht beweisen wollen.

Für \gamma > 90° liegt die einzuzeichnende Höhe ausserhalb des Dreiecks. Die Vorgehensweise ist ganz ähnlich wie oben, nur dass wir diesmal den Nebenwinkel \gamma' von \gamma verwenden und die Beziehung \cos \gamma' = \cos (180° - \gamma) = -\cos \gamma ausnutzen.

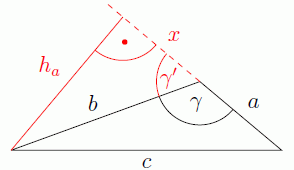
Wir zeichnen die Höhe h_a auf die Verlängerung der Seite a ein. Das Stück, um das wir damit die Seite a verlängern, nennen wir x. Im oberen Teildreieck berechnen wir mit dem Kosinus-Seitenverhältnis die Länge von x und dann mit dem Satz des Pythagoras die Länge der Höhe h_a. Schließlich ermitteln wir wieder mit dem Satz des Pythagoras aus x + a und h_a die gesuchte Seite c:

\begin{align*} x &= b \nachhilfe \cos (180° - \gamma) = -b \nachhilfe \cos \gamma &&\text{mit dem Kosinus-Seitenverhältnis} \\[3pt] h_a^2 &= b^2 - x^2 = b^2 - b^2 \nachhilfe \cos^2 \gamma &&\text{nach Pythagoras}\\[3pt] c^2 &= h_a^2 + (a+x)^2 &&\text{nach Pythagoras} \\[3pt] &= b^2 - b^2 \nachhilfe \cos^2 \gamma + (a - b \nachhilfe \cos \gamma)^2 &&\text{für $h_a^2$ und $x$ eingesetzt}\\[3pt] &= b^2 - b^2 \nachhilfe \cos^2 \gamma + a^2 - 2ab \nachhilfe \cos \gamma + b^2 \cos^2 \gamma &&\text{mit der binomischen Formel aufgelöst} \\[3pt] &= b^2 + a^2 - 2ab \nachhilfe \cos \gamma. \end{align*}

Anwendungsbeispiele zur Dreiecksberechnung

Gegeben sei ein Dreieck mit b = 12, c = 8 und \alpha = 24°. Wir rechnen

a^2 = b^2 + c^2 - 2bc \nachhilfe \cos \alpha = 12^2 + 8^2 - 2 \nachhilfe 12 \nachhilfe 8 \nachhilfe \cos 24° \approx 32{,}6

Also ist a = \sqrt{32{,}6} \approx 5{,}7.

Da wir nun über alle 3 Seiten verfügen, können wir die restlichen Winkel ebenfalls mit dem Kosinussatz berechnen. Z.B.:

\cos \gamma = \frac{a^2 + b^2 - c^2}{2ab} \approx \frac{32{,}6 + 144 - 64}{2 \nachhilfe 5{,}7 \nachhilfe 12} \approx 0{,}8217134388.

Also ist \gamma \approx 34{,}74°.