Mathematik Lernzentrum
Dipl.-Math. W. Köpper
Mathematik verstehen in der Mathe Nachhilfe

Hier klicken und
Nachhilfe in Mathematik
kostenlos kennenlernen

Der Sinussatz

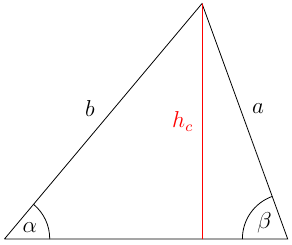
Dreieck mit Höhe auf c

In dem nebenstehenden Dreieck gilt

\frac{h_c}{b} = \sin \alpha \qquad \text{ und } \qquad \frac{h_c}{a} = \sin \beta.

Durch Auflösen beider Gleichungen nach h_c und Gleichsetzen folgt

b \nachhilfe \sin \alpha = h_c = a \nachhilfe \sin \beta

und damit

\frac{a}{\sin \alpha} = \frac{b}{\sin \beta}

Indem wir die Höhe auf a einzeichnen, erhalten wir auf gleiche Weise

\frac{b}{\sin \beta} = \frac{c}{\sin \gamma}

insgesamt also

\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma}
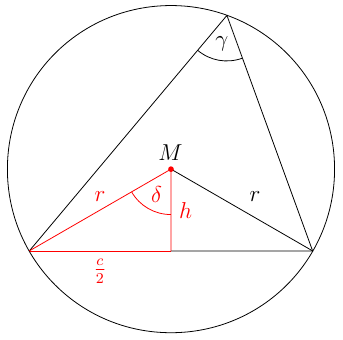
Dreieck mit Umkreis

In der nebenstehenden Skizze ist der Umkreis eines Dreiecks mit Mittelpunkt M und Radius r eingezeichnet. Da die Höhe h in dem gleichschenkligen Dreieck mit Schenkellänge r die Basis c dieses Dreiecks halbiert, gilt

\frac{\frac{c}{2}}{r} = \sin \delta \quad \Leftrightarrow \quad \frac{c}{\sin \delta} = 2r.

Nach dem Umfangswinkelsatz ist der Mittelpunktswinkel 2 \nachhilfe \delta über der Kreissehne c aber doppelt so groß wie der Umfangswinkel \gamma, also 2 \nachhilfe \delta = 2 \nachhilfe \gamma und damit \delta = \gamma.

Insgesamt erhalten wir also

\frac{c}{\sin \gamma} = 2r

Der Quotient im Sinussatz ist damit der doppelte Umkreisradius, also der Umkreisdurchmesser.

Anwendungsbeispiel zum Sinussatz

Der Sinussatz kann immer dann besonders vorteilhaft angewendet werden, wenn in einem beliebigen Dreieck zwei Winkel (und damit natürlich auch der dritte) sowie eine Seite bekannt sind. Seien zum Beispiel

\alpha=30° \qquad \beta=50° \qquad b=3 \text{ cm.}

Dann gilt

\frac{a}{\sin 30°} = \frac{3}{\sin 50°},

also

a = \frac{3}{\sin 50°} \nachhilfe \sin 30° \approx1{,}96 \text{ cm}.

Aus der Winkelsumme von 180° im Dreieck ergibt sich \gamma = 100° und damit

\frac{c}{\sin 100°} = \frac{3}{\sin 50°} \Longleftrightarrow c = \frac{3}{\sin 50°} \nachhilfe \sin 100° \approx 3{},86 \text{ cm}.

Etwas komplizierter kann es werden, wenn zwei Seiten und ein Winkel gegeben sind. Ist der Winkel nicht von den beiden gegebenen Seiten eingeschlossen, dann kann uns der Sinussatz auch hier weiterhelfen. Seien zum Beispiel

a=5 \text{ cm} \qquad b=7 \text{ cm.} \qquad \beta=50°.

Dann gilt

\frac{5}{\sin \alpha} = \frac{7}{\sin 50°} \Longleftrightarrow \sin \alpha = \frac{\sin 50°}{7} \nachhilfe 5 \approx 0{,}5471746.

Ein Taschenrechner liefert uns \alpha \approx 33{,}17°. Wegen \sin \alpha = \sin(180°-\alpha) wissen wir aber, dass auch \sin(180°-33{,}17°) \approx 0{,}5471746 gilt. Es kommt hier also noch der weitere Winkel \alpha \approx 146{,}83° in Frage. Da jedoch \beta = 50° ist und 146{,}83° + 50° > 180° ist, scheidet diese zweite Lösung gleich wieder aus. Andernfalls müssten wir unsere Rechnung gleichermaßen für diese zweite Lösung fortsetzen. Hier ergibt sich nun

\gamma = 180° - \alpha - \beta \approx 180°-33{,}17-50 = 96{,}83°

und wir errechnen die zugehörige Seite c wie im Beispiel oben.